Многокритериальный подход к обоснованию алгоритма запуска многоприводного забойного скребкового конвейера с двухскоростными электродвигателями
Автор:В.П. Кондрахин, Ю.А. Зубова, Е.Л. Ткаченко
Источник: Статья поступила в редакцию 10.05.2014 года.
Автор:В.П. Кондрахин, Ю.А. Зубова, Е.Л. Ткаченко
Источник: Статья поступила в редакцию 10.05.2014 года.
УДК 622.647.1
В.П. Кондрахин (д-р техн. наук, проф.),
Е.Л. Ткаченко (бакалавр),
Ю.А. Зубова (бакалавр)
Донецкий национальный технический
университет
Многокритериальный подход к обоснованию
алгоритма запуска многоприводного забойного скребкового конвейера с двухскоростными
электродвигателями
В работе на основе вычислительных экспериментов установлены
особенности влияния параметров пусковых режимов многоприводных скребковых конвейеров
с двухскоростными электродвигателями на
нагрузку приводов и тягового органа. Обоснованы оптимальные режимы запуска
двухскоростных многоприводных скребковых конвейеров на первую (низкую) и
перехода на вторую (высокую) скорости с точки зрения равномерного распределения
нагрузки между приводами , минимизации максимальных значений натяжений
тягового органа и пускового тока, а также возможности реализации «тяжелого» пуска.
Ключевые слова: многоприводной конвейер, двухскоростной электродвигатель, алгоритм, пуск, тяговый орган, привод, скорость.
Проблема и ее связь с научными или практическими задачами.
В составе многодвигательных приводов современных
высокоэнерговооруженных забойных скребковых конвейеров используются
двухскоростные асинхронные электродвигатели [1].
Для таких конвейеров актуальной является задача выбора рациональных последовательности
и соответствующих задержек времени при пуске двигателей на первую (низкую НС) и
последующем переходе на вторую (высокую ВС) скорости [2,3]. При этом критериями
выбора должны являться не только равномерность распределения нагрузки между приводами,
но и величины максимальных значений натяжения тягового органа при пуске,
обеспечение возможности «тяжелого» пуска в условиях экстремально больших
значениях сопротивления движению тягового органа, а также величина суммарного
пускового тока при переходе на высокую скорость.
Анализ исследований и
публикаций.
Для оптимальной
адаптации режима пуска двухскоростных конвейеров к работе в заданных условиях
разработана математическая модель, которая позволяет исследовать процесс
формирования пусковых нагрузок в приводах и тяговом органе [4,5].
Постановка задачи.
Целью настоящей работы
является повышение
эффективности эксплуатации двухскоростных многоприводных забойных скребковых
конвейеров за счет обоснованного выбора оптимального алгоритма их запуска на
основе многокритериального подхода, который обеспечивает равномерное
распределение нагрузки между приводами, минимальные тяговые усилия цепи и
пусковые токи, а также возможность «тяжелого» пуска при экстремально высоких
значениях сил сопротивления.
Изложение материала и результаты.
Основным методом исследований в настоящей работе
является метод математического моделирования с использованием математической
модели многоприводного скребкового забойного конвейера с двухскоростными
асинхронными электродвигателями [4].
Для изучения закономерностей формирования максимальных натяжений
тягового органа скребкового конвейера в пусковых режимах была проведена серия
вычислительных экспериментов, в которых для двух- и трёхприводных конвейеров
различной длины и для различных углов транспортирования моделировался процесс
запуска конвейера с различными последовательностями и задержками времени пуска
хвостового и головных приводов.
Рассмотрим процесс формирования
натяжения тяговой цепи двухприводного скребкового конвейера при пуске на первую (низкую) скорость
по найденному в работе [2] алгоритму,
обеспечивающему равномерность распределения нагрузки между приводами. При анализе приняты следующие обозначения: Rp1;
Rx1-
натяжения в тяговом органе в точках набегания на звезды, соответственно,
рабочей и холостой ветви. Rp7; Rx7 -
натяжения в тяговом органе в точках сбегания со звезд, соответственно, рабочей
и холостой ветви, Δt1 - задержка времени между пуском хвостового и головного
электродвигателя.
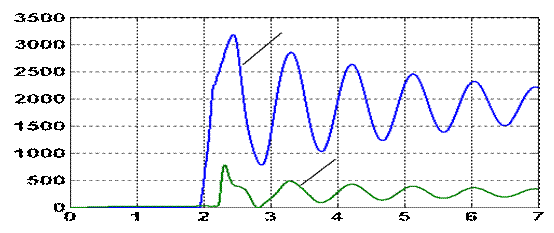
На рис. 1 в качестве примера приведены диаграммы
изменения натяжения цепи в процессе пуска на НС при оптимальном (с точки зрения
равномерности распределения нагрузок между приводами) значении Δt1 = 0,94с
двухприводного конвейера КСД27 длиной L=200 м, транспортирующего горную массу вверх под углом
α = 15º. Погонная масса груза на полотне конвейера
принималась q=90 кг/м.
На рисунке 1 численные значения натяжений цепи даны приведенными к валу
электродвигателя, таким образом для перехода к фактическим натяжениям эти
значения следует умножить на передаточное отношение редуктора привода, для
рассматриваемого случая 33,43.
Rp, Н t, c Rp1 Rp7
Rx, Н t, c Rх7 Rх1

Рисунок 1 – Диаграммы изменения
приведенного к валу электродвигателя натяжения тяговой цепи на рабочей и
холостой ветвях при пуске двухскоростного двухприводного конвейера КСД27 длиной
200м (Δt1 =Δt1опт= 0,94с).
В рассмотренном примере на рабочей ветви приведенные к
валу электродвигателя максимальные значения натяжений цепи в крайних точках
равно Rp1=3200Н; Rp7=700Н, а на холостой ветви: Rx1=2300H; Rx7=1000H, причем максимальные значения натяжения цепи в
различных точках контура формируются почти одновременно через 1,1…1,3 с после
запуска хвостового электродвигателя.
В таблице 1 даны полученные в результате
вычислительных экспериментов фактические (не приведенные) значения максимальных
натяжений цепи при пусках двухприводного конвейера по различным алгоритмам.
Таблица1. - Максимальное
натяжение (Н) тяговой цепи при пуске двухприводного конвейера по оптимальному и
неоптимальному алгоритму.
|
|
Максимальное натяжение, кН |
|||||||||
|
L=100м |
L=200м |
L=300м |
||||||||
|
α= -15º |
α=0º |
α=15º |
α= -15º |
α=0º |
α=15º |
α= -15º |
α=0º |
α=15º |
||
|
Δt1=
Δt1опт |
0,25 |
0,85 |
0,81 |
0,05 |
1,19 |
0,94 |
0,06 |
1,6 |
1,12 |
|
|
Rp1ф |
150 |
114 |
83,6 |
251 |
177 |
107 |
364 |
251 |
137 |
|
|
Rp7ф |
30,0 |
23,4 |
16,7 |
33,4 |
30,0 |
23,4 |
50,1 |
33,4 |
26,7 |
|
|
Rx1ф |
73,5 |
63,5 |
50,1 |
134 |
104 |
76,9 |
204 |
147 |
96,9 |
|
|
Rx7ф |
56,8 |
36,7 |
10,0 |
96,9 |
66,8 |
33,4 |
147 |
86,9 |
50,1 |
|
|
Δt1≠
Δt1опт |
0,3 |
1,0 |
0,7 |
0,2 |
0,5 |
1,5 |
0,1 |
1,4 |
1,3 |
|
|
Rp1ф |
150 |
114 |
83,6 |
251 |
177 |
107 |
364 |
251 |
137 |
|
|
Rp7ф |
30,0 |
23,4 |
16,7 |
33,4 |
30,0 |
23,4 |
50,1 |
33,4 |
26,7 |
|
|
Rx1ф |
96,9 |
100 |
50,1 |
167 |
70,2 |
147 |
214 |
120 |
114 |
|
|
Rх7ф |
73,5 |
83,6 |
10,0 |
127 |
16,7 |
107 |
150 |
63,5 |
50,1 |
|
Из таблицы 1
следует, что максимальные нагрузки в рабочей ветви при запусках по оптимальному
и неоптимальному алгоритму одинаковы, то есть практически не зависят от
величины Δt1опт. Максимальные значения нагрузки в холостой ветви
существенно изменяются при изменении алгоритма запуска. В большинстве случаев
максимальные значения натяжения цепи для холостой ветви при пуске по
оптимальному алгоритму существенно меньше, чем при пуске с другими значениями
времени задержки. Исключение составляет случай, когда конвейер длиной
Таким образом, найденные оптимальные с точки зрения
равномерности распределения нагрузки между приводами алгоритмы пуска двухприводного
конвейера на первую скорость обеспечивают наименьшие нагрузки на тяговую цепь в
пусковых режимах.
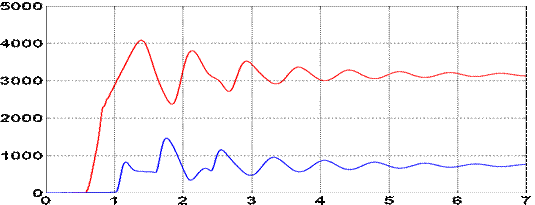
Рассмотрим теперь пуск трехприводного конвейера. На рис. 2. в качестве примера приведены
диаграммы изменения натяжения цепи в процессе пуска по оптимальному (с точки
зрения равномерности распределения нагрузок между приводами) алгоритму
загруженного на всю длину трёхприводного конвейера КСД27 длиной L=
Из рис. 2 следует, что приведенные к валу
электродвигателя максимальные значения натяжений при пуске на рабочей ветви
составляют 4100Н и 1400Н, а на холостой − 500Н, 2700Н.
t, c Rp7 Rp1 Rp, Н
t, c Rх7 Rх1 Rx, Н
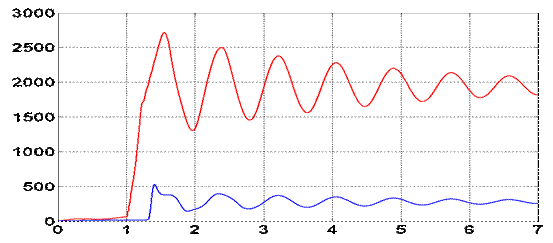
Рисунок 2. – Диаграмма
изменения приведенного к валу электродвигателя натяжения на рабочей и холостой
ветви при пуске двухскоростного трехприводного конвейера КСД27 длиной 300м
(Δt1 =Δt1опт= -0,42с).
Проводилась серия вычислительных экспериментов для
различных значений длины и угла транспортирования, в которых определялись
максимальные значения натяжений цепи при пуске по оптимальному (с точки зрения
распределения нагрузки между приводами) и некоторым другим алгоритмам.
Результаты этих экспериментов в виде фактических (не приведенных) максимальных
значений натяжения цепи в характерных точках представлены в таблице 2.
Таблица 2 – Максимальные значения натяжения в
характерных точках цепного контура при пуске
|
|
Максимальное натяжение,
кН |
|||||||||
|
L=200м |
L=300м |
L=400м |
||||||||
|
α= -15º |
α=0º |
α=15º |
α= -15º |
α=0º |
α=15º |
α= -15º |
α=0º |
α=15º |
||
|
Δt1=
Δt1опт |
0,11 |
0,15 |
-0,18 |
0,18 |
0,42 |
-0,42 |
0,3 |
0,7 |
-0,73 |
|
|
Rp1ф |
251 |
181 |
110 |
472 |
241 |
137 |
468 |
318 |
170 |
|
|
Rp7ф |
36,8 |
26,7 |
46,8 |
60,2 |
36,8 |
46,8 |
66,8 |
50,0 |
53,5 |
|
|
Rx1ф |
93,0 |
70,3 |
73,5 |
140 |
106,9 |
90,2 |
130 |
130 |
113 |
|
|
Rx7ф |
53,5 |
26,7 |
16,7 |
83,3 |
48,4 |
16,7 |
53,5 |
53,5 |
17,3 |
|
|
Δt1 ≠
Δt1опт |
-0,25 |
-0.15 |
0,3 |
-0,7 |
-0,5 |
0,2 |
-0,5 |
-0,7 |
0,8 |
|
|
Rp1ф |
250,7 |
180 |
110 |
364 |
241 |
137 |
468 |
318 |
170 |
|
|
Rp7ф |
36,8 |
26,7 |
16,7 |
60,2 |
36,8 |
17,7 |
66,8 |
50 |
26,7 |
|
|
Rx1ф |
73,5 |
70,3 |
100 |
83,6 |
87,4 |
147 |
110 |
110 |
150 |
|
|
Rх7ф |
16,7 |
13,5 |
51,8 |
16,7 |
16,7 |
87 |
16,7 |
16,7 |
63,5 |
|
Отрицательные значения параметра Δt1 означают,
что сначала запускаются головные привода, а затем – хвостовой привод. Из
таблицы видно, что не всегда оптимальный алгоритм запуска конвейера, при
котором нагрузка между приводами распределяется равномерно, является также
оптимальным с точки зрения максимальных натяжений холостой ветви тяговой цепи.
При транспортировке груза вниз (а это наиболее распространенный на практике
случай), нагрузки в холостой ветви при пуске по оптимальному, с позиций
равномерности распределения нагрузок, алгоритму оказываются больше, чем при
пуске по другим алгоритмам.
Однако максимальные нагрузки, которые определяют
прочность цепи, формируются не на холостой, а на рабочей ветви и практически не
зависят от выбора алгоритма запуска. Поэтому найденные значения Δt1опт является
рациональным и с точки зрения прочности и надежности тяговой цепи.
Найденные оптимальные значения задержки времени определены
для номинальных значений коэффициента сопротивления на груженой ветви W2max=0,5.
Однако при эксплуатации конвейера зачастую возникает необходимость запуска при
экстремально высоких значениях этого коэффициента. Например, при
транспортировании влажной горной массы после длительной остановки конвейера
груз ссыхается, «цементируется» и уплотняется, что резко повышает сопротивление
движению.
В качестве примера рассмотрим представительный случай запуска
двухприводного конвейера длиной
При изменении времени задержки изменяется также предельное
значение обобщенного коэффициента сопротивления на груженой ветви W2max.
Характер этой зависимости для рассматриваемого примера представлен на рис.3.
W2max Δt1, с
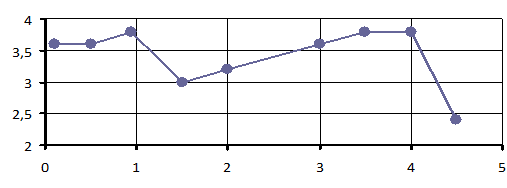
Рисунок 3. – Зависимость
максимальных допустимых значений обобщенного коэффициента сопротивления на
груженой ветви, при
которых привод конвейера ещё запускается, от времени задержки
Δt1.
Указанная зависимость достаточно сложная, имеется 2
максимума, примерно равных по величине. При этом один из максимумов
соответствует найденному ранее оптимальному значению времени задержки Δt1 = 0,94с.
Из этого следует, что найденные оптимальные с точки зрения равномерности
распределения нагрузки между приводами алгоритмы пуска являются рациональными и
с позиций обеспечения «тяжелого» пуска конвейера.
![]() Аналогичный анализ выполнен применительно к
трехприводному конвейеру для представительного случая транспортирования горной
масс вверх с углом транспортирования 15º при длине конвейера
Аналогичный анализ выполнен применительно к
трехприводному конвейеру для представительного случая транспортирования горной
масс вверх с углом транспортирования 15º при длине конвейера
Из рис. 4 следует, что для трехприводных конвейеров
предельное значения коэффициента сопротивления, при котором пуск еще возможен,
увеличивается на величину до 30% и более по мере роста задержки времени ∆t1. Следовательно, если пуск двигателя не
состоялся из-за чрезмерно больших значений сил сопротивления движению,
необходимо при повторной попытке увеличить значение Δt1 (в
рассматриваемом случае до 3,5 с и более).
Δt1, с W2max
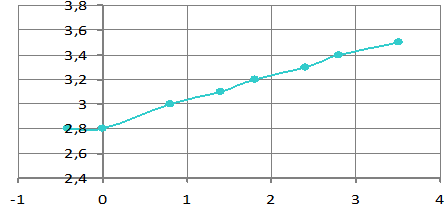
Рисунок 4. – График
зависимости предельных допустимых значений обобщенного коэффициента
сопротивления W2max на груженой ветви, при которых привод конвейера ещё
запускается, от времени задержки ∆t1
Рассмотрим закономерности перехода многоприводных
двухскоростных забойных конвейеров на высокую скорость (ВС). Существенное
влияние на процесс формирования нагрузки приводов при переходе на высокую
скорость оказывает величина интервала времени Δt2 между
подачей напряжения на соответствующие обмотки статоров хвостового и головных
приводов. Эта величина должна быть по возможности минимальной (примерно 0,05с),
что обеспечивает равномерное распределение нагрузки между приводами. Однако в
реальных условиях при уменьшении Δt2 суммарное
значение пусковых токов (особенно при наличии трёх приводов) становится слишком
большим для большинства характерных условий энергоснабжения забойных скребковых
конвейеров.
На рисунке 5, в качестве примера приведена диаграмма
процесса пуска на низкую и высокую скорости по оптимальному алгоритму загруженного
на всю длину двухприводного конвейера КСД27 длиной
На рисунке приняты обозначения Мх,
Мг – приведенные к валу электродвигателя моменты в хвостовом и
головном приводах, Iх , Iг, ∑I – токи соответственно хвостового,
головного и суммарный ток двух приводов.
t, с М,Нм Мх Мг
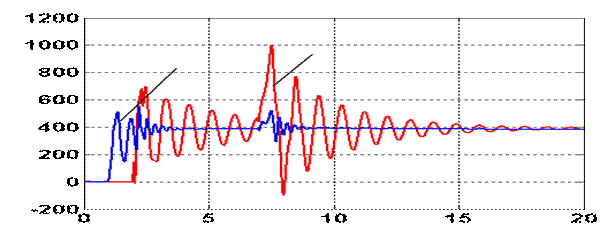
I,А t, с Iх Iг ∑I

Рисунок 5. – Диаграммы процесса пуска по оптимальному
алгоритму (Δt1 = 0,94с, Δt2 = 0,05с)
загруженного на всю длину двухприводного конвейера КСД27 длиной
Как видно из рисунка 5, нагрузка распределяется между
приводами примерно одинаково. При этом через 6 с после начала пуска на НС первым
запускается головной двигатель на ВС, затем через интервал времени Δt2 = 0,05 с
происходит запуск хвостового привода на ВС. Максимальное значение суммарного
тока двух электродвигателей составляет ∑Imax = 1455 А.
Проводилась серия вычислительных экспериментов, в
результате которых были установлены максимальные
значения ∑Imax суммарных пусковых токов при переходе на ВС в зависимость от времени задержки ∆t2.
Результаты приведены на рис. 6. Из графика следует,
что минимальное значение ∑Imax = 1365 А соответствует Δt2=0,25с.
Δt2, с ∑Imax, А
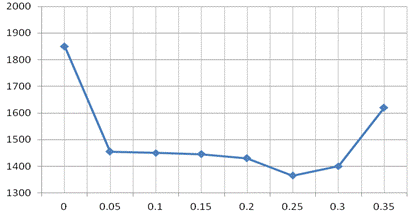
Рисунок 6.- График зависимости суммарного пускового
тока при переходе двухприводного конвейера на ВС от времени задержки ∆t2.
Результаты анализа пусковых токов при переходе на
высокую скорость трёхприводного конвейера длиной
Δt2, с ∑Imax, А

Рисунок 7. - График зависимости суммарного
пускового тока при переходе трехприводного конвейера на ВС от времени задержки
∆t2
Из рис. 7 следует, что при одновременном
включении всех трёх приводов (∆t2=0)
суммарное значение токов составляет – ∑I=2350 А. При задержки времени
∆t2 в диапазоне от 0,05с до 0,2с, значения суммарных токов минимальные
∑I = 1800…1850 А. Оптимальной алгоритм перехода на высокую скорость предполагает
переход сначала головных электродвигателей, а затем через ∆t2 =
0,05с переход на ВС хвостового привода, так как в этом случаи нагрузка между
приводами распределяется практически равномерно.
Выводы и направления дальнейших исследований. Найденные
в работах [2,3] значения задержки времени между
пусками хвостового и головного приводов двухскоростных забойных скребковых
конвейеров на низкую скорость являются
оптимальными не только с точки зрения равномерности распределения нагрузки
между приводами, но также с точки зрения формирования максимальных нагрузок
тяговой цепи и с точки зрения обеспечения «тяжелого» пуска конвейера с
экстремально большими значениями сил сопротивления движению.
При
переходе на высокую скорость время задержки Δt2 между пусками
хвостового и головного привода следует принимать по возможности минимальным,
однако при этом суммарный пусковой ток обоих приводов может быть слишком
большим для принятой системы энергоснабжения. За счет повышения Δt2
до 0,05…0,25 с можно уменьшить суммарный пусковой ток на 6-30% по сравнению с
пусковым током одновременного перехода всех двигателей на высокую скорость.
Полученные в работе результаты позволяют более обоснованно
определять алгоритм запуска на низкую скорость и перехода на высокую скорость забойных
скребковых конвейеров для угольной промышленности в соответствии с горнотехническим
условиям эксплуатации конкретной машины.
Список литературы.
1.
Андреев Г.В., Косарев И.В. Скребковые
конвейеры нового технического уровня – Уголь Украины. - №9, 2003. - С. 30-34
2.
Кондрахин В.П. Оптимизация
алгоритма пуска многоприводных двухскоростных забойных конвейеров / В. П.
Кондрахин, Н.И. Стадник, В.В. Косарев, И.В. Косарев // Форум гірників-2009:
матеріали міжнар. конф., 30 верес.-3 жовт.2009 р.- Дніпропетровськ: НГУ, 2009.-
С.190-196
3. Кондрахин В.П., Стадник Н.И. Пусковые режимы трехприводных двухскоростных забойных конвейеров . - Уголь Украины. - №5, 2011.- С. 45-48
4. Кондрахин В.П. Математическая модель для исследования нагрузок в двухскоростном многодвигательном приводе и тяговом органе скребкового забойного конвейера Кондрахин В.П., Мельник А.А., Косарев В.В., Стадник Н.И., Косарев И.В. / Наукові праці Донецького національного технічного університету, вип. 16 (142), Серія: гірничо-електромеханічна, Донецьк, 2008, с. 132-140
5. Обоснование конечно-елементной модели тягового органа скребкового конвейера // Кондрахин В.П., Борисенко В.Ф., Мельник А.А. и др.- Наукові праці Донецького національного технічного університету, вип.99 , Серія: гірничо-електромеханічна, Донецьк, 2005, с.97-103
Стаття надійшла до редколегії 10.05.2014
В.П. Кондрахін, К.Л. Ткаченко, Ю.А. Зубова. Донецький національний технічний університет
Багатокритерійний
підхід до обґрунтування алгоритму запуску багато приводного забійного
скребкового конвеєра з двохшвидкісними єлектродвигунами
У роботі на основі обчислювальних експериментів встановлено
особливості впливу параметрів пускових режимів багатоприводних скребкових
конвеєрів з двохшвидкісними електродвигунами на навантаження приводів і
тягового органу. Обґрунтовано оптимальні режими запуску двошвидкісних багатоприводних скребкових конвеєрів на першу ( нижчу) і
переходу на другу (високу) швидкості з
точки зору рівномірного розподілу навантаження між приводами , мінімізації
максимальних значень натягу тягового органу та пускового струму , а також
можливості реалізації «важкого» пуску .
Ключові слова: багатоприводний конвеєр, двохшвидкісний электродвигун, алгоритм, тяговий орган, привод, швидкість.
V.Kondrakhin, К.Tkachenko,
Multicriteria approach to the justification of the start sequence of the
armored face conveyor with two-speed motors
Features of influence of
parameters conveyor’s starting modes to loads of the drive units and traction
body are found out in this paper based on computational simulation experiments.
The optimal two-speed startup modes of the multidrive armored face conveyor to
the first (lowest) and the transition to the second (higher) speed have been
explained in terms of load balancing between drives ,
minimizing the maximum values of pulling unit tension and starting current , as
well as the feasibility of "heavy" start . It was found out that during the transition to high speed delay Δt2 should be as small as
possible, but the total inrush current of all drives may be too large for the
established system of power consumption.
The results allow a reasonably
determine the algorithm of the armored face conveyor
starting to the first (lowest) and the transition to the second
(higher) speed for the
coal industry in accordance with the mining conditions of
operation of a concrete machine.
Keywords: Multi-drive conveyor, two-speed motor,
start algorithm, traction
body, drive speed
© Кондрахин В.П., Ткаченко Е.Л.,
Зубова Ю.А.,
2014